Data details¶
The challenge this year focuses on the effect of the local reconstruction accuracy on the quality of connectivity reconstruction. The phantom consists in a set of fiber bundles, that connect one area of the “cortex” to another. There is a wide range of configurations (branching, crossing, kissing), fiber bundles radii, and fiber geometry.
Signal simulation¶
Given the fiber configurations, the diffusion MR signal is simulated in each voxel. To account for the partial volume effect (multiple fiber compartments within the same imaging voxel), we use an approach similar to the Numerical Fiber Generator [Close2009].
As for the local model of diffusion, the signal is simulated considering hindered and restricted diffusion, to account for extra-axonal and intra-axonal diffusion. Finally, depending on the position in space, there is also an isotropic compartment, to account for the CSF contamination close to the ventricles in brain imaging.
Noise simulation¶
The magnitude MR signal is corrupted by Rician noise. If 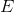 is
the noise-free diffusion weighted signal, then the signal is simulated as
is
the noise-free diffusion weighted signal, then the signal is simulated as
where 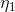 and
and 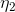 , are independent, zero-mean Gaussian
distributed with the same covariance
, are independent, zero-mean Gaussian
distributed with the same covariance 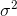 .
.
Data format¶
The simulated signal for a given SNR and a given acquisition scheme is provided as a 4D Nifti image.
References
| [Close2009] | Thomas G. Close et al., A software tool to generate simulated white matter structures for the assessment of fibre-tracking algorithms, NeuroImage (2009). |